How to interpret results from a randomized controlled experiment correctly

Written By Rick Bruner

Screenshot of reporting from Central Control’s platform Experiment Designer

In the Research Wonks forum (recommended for all marketing analysts: visit researchwonks.com for details), I was asked my opinion on a thread titled "Does stat testing encourage the wrong decisions?" The heart of the question was how to interpret tests that aren't deemed quite "statistically significant," yet the profit value of the product is very high and purchase rates are very low (e.g., boats, solar panels, home owner's insurance).

Here is a modified version of my response, which is really a bit of an explainer on experimentation statistics themselves. As I noted in an earlier post in the forum, all of this pertains to well-constructed randomized controlled trials (RCT). If your definition of a test is relying on synthetic controls, matched markets or other quasi experimental methods, I'm much more skeptical of the results overall. More on that below.

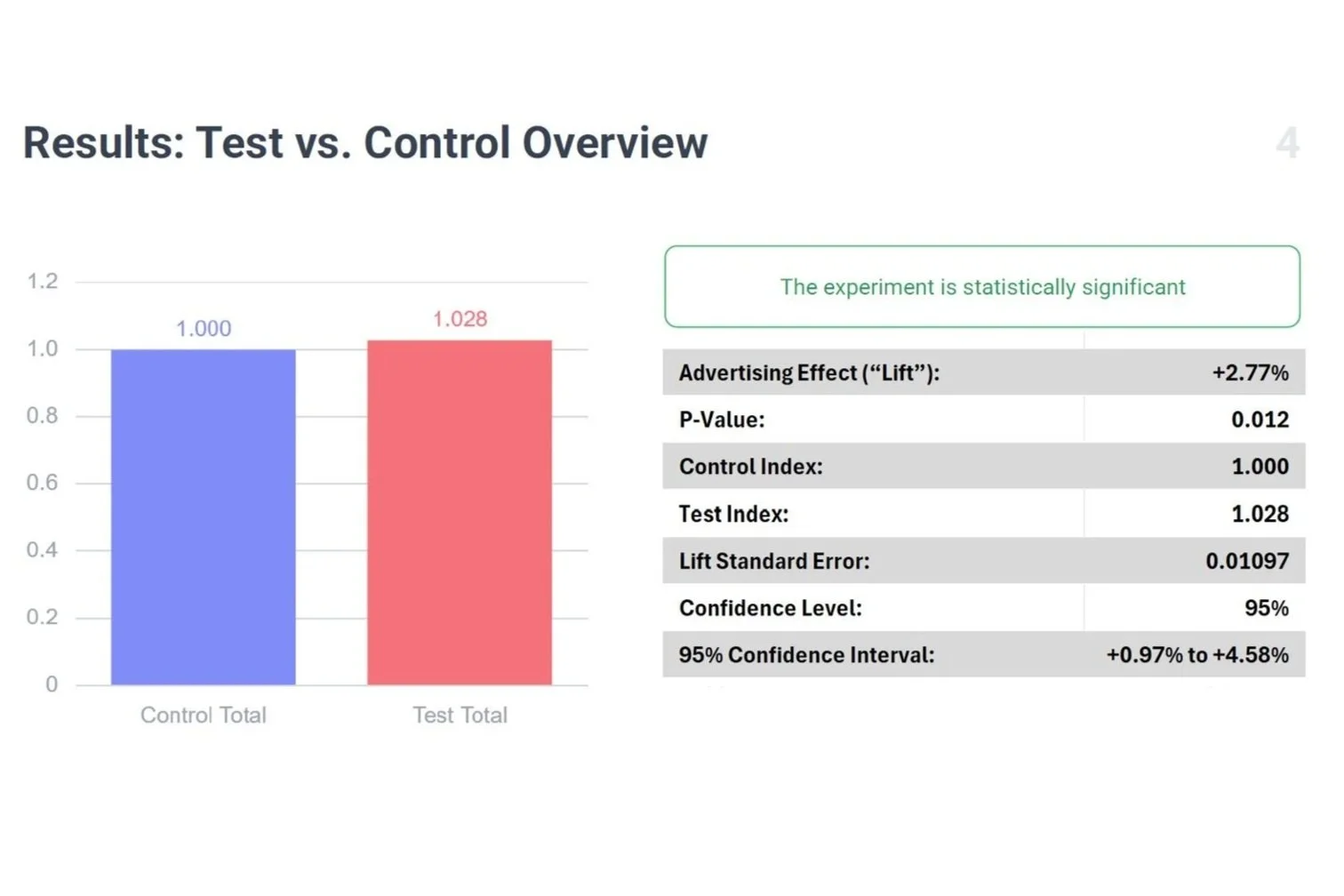
Marketers often fixate on the 95% confidence level as the determinant of whether a test was “valuable” or not, when that's only one component of what makes an experiment result meaningful. It’s also often misunderstood.

Confidence level (CL) measures the likelihood that a result is a false positive — a Type I error. It’s not really saying “there was almost certainly a positive lift.” It’s saying that if you ran the test under the same conditions an infinite number of times, about 5% of the time you’d see a lift when in fact there wasn’t one. In other words, a false positive (Type I error).

The p-value of the test has an inverse relationship to the CL: a p-value under 0.05 indicates significance at the 95% CL.

It goes without saying that this foundation of statistics clearly describes an impossibility: the threshold of infinity notwithstanding, in advertising, test conditions are always unique, where each is a one-time snapshot of a combination of the creative, offer, audience, media, point in time, etc. But statistics is theoretical stuff. In a class on regression I once took, the professor described the concept of a “parent population,” being the theoretical infinite number of samples you could draw under the model, and the “daughter population,” which is the single sample you actually observed. The p-value, and most other statistical metrics, refer back to the likelihood that your daughter population correctly represents the “true” (theoretical) population.

Power describes the likelihood that your test will detect a positive result if one really exists. The common convention in experiment design is 80% power, which can feel low, since it’s answering the critical question: “Will I actually detect a lift if it’s there?” For experiments supporting high-stakes decisions, you might power for 90%. Unfortunately, power isn’t something you get as a marker in the results (like the p-value); it’s a design property, determined up front by inputs including sample size and the effect size you care about.

The maddening part is: with 80% power, if you fail to reject the null (i.e., no significant lift detected), there’s still a 1 in 5 chance that a true lift of the size you powered for was actually present, but your test missed it due to random chance, such as an unlucky draw of randomly assigned experiment units, ill-winds blowing from the south, etc. This is a Type II error, a false negative.

Which leads to three other important topics: confidence intervals, Bayesian thinking, and the value of an accumulated body of evidence.

Confidence intervals (CIs) are often neglected in superficial reporting of test results, but they’re crucial for interpretation. A CI shows the plausible range of effect sizes given your data, which bears on the original question in the Wonks forum: how to interpret significance in the case of high-value, low incidence transactions.

Ideally, results should look like: “Estimated lift = 5%, p = 0.04, 95% CI = +0.2% to +9.8%.” The p-value tells us the result just clears the 95% confidence level (so the false-positive risk is controlled at 5%). The CI tells us the range is fairly wide: the true lift could be as small as +0.2% or as large as +9.8%. So, even with a test that is "significant" at a 95% CL, the actual sales impact could vary widely, which is key for ROI. The measured effect size is really just a point estimate.

The formula is: CI = Estimate ± (Zα/2 × SE)

If you're using a 90% (or 80%) confidence level, and the lift is deemed positive but the p-value is > 0.05, then the 95% CI will straddle zero — meaning the data are consistent with no effect, a small positive effect, or even a negative effect. That’s why 95% CL is a useful rule of thumb, as a p-value of less than 0.05 assures the whole range of the CI will be greater than zero.

Beware the temptation to run one-tailed tests in ad experiments, where the presumption is the effect could only be positive. Ads can backfire. Think of the X10 camera from years ago — pioneer of the notorious pop-under ad format — that so annoyed people it arguably created negative lift. That logic also shows up in uplift modeling, where one audience segment is “sleeping dogs,” whose purchase likelihood can be harmed by advertising.

Bayesian analysis offers a more flexible interpretation than the rigid frequentist thresholds. Most MMM models today are Bayesian. In that mindset, even a p-value of 0.15 can be treated as evidence pointing toward a positive lift — not definitive, but suggestive, and potentially worth acting on depending on priors and expected ROI.

Finally, I always stress that the greatest confidence comes not from any one test but from a body of evidence built through repeated RCTs. In the hierarchy of evidence, the only thing stronger than a single well-run RCT is a meta-analysis of many of them. The closer you get to that “infinity of tests,” the more solid your knowledge becomes. Big advertisers, agencies, MMM shops, and publishers who accumulate 10s, then 100s, then 1000s of RCTs build a serious moat in their understanding of what really works across ad formats, CTAs, publishers, channels, product categories, and so on.

Of course, as I said at the top of this essay, all of these statistics are on shaky ground if your “testing” relies on synthetic controls, matched markets, propensity scores, machine learning, or other forms of quasi-experiments. Quasi-experiments can be useful if true RCTs are infeasible (rare in advertising) and/or if the expected effect size is very large. But if you’re chasing a 1-10% effect with a quasi-experiment, I wouldn’t bet the farm.

I wrote recently on LinkedIn that with enterprise AI systems poised to take over media planning, there’s a real danger those systems will train on quasi-experimental results — which pervade ROI measurement in advertising — and institutionalize bad learnings, creating a huge “knowledge debt” that will take years to unwind. Garbage in, garbage out.

Recommended further reading on the subject:

Rick Bruner
Next

NEW WHITEPAPER: How to Design a Geographic Randomized Controlled Trial